خصوصيتك مهمة بالنسبة لنا. لهذا السبب ، قمنا بتطوير سياسة الخصوصية التي تصف كيفية استخدامنا لمعلوماتك وتخزينها. يرجى قراءة سياسة الخصوصية الخاصة بنا وإعلامنا إذا كان لديك أي أسئلة.

جمع واستخدام المعلومات الشخصية

تشير المعلومات الشخصية إلى البيانات التي يمكن استخدامها لتحديد هوية شخص معين أو الاتصال به.

قد يُطلب منك تقديم معلوماتك الشخصية في أي وقت عند الاتصال بنا.

فيما يلي بعض الأمثلة على أنواع المعلومات الشخصية التي قد نجمعها وكيف يمكننا استخدام هذه المعلومات.

ما هي المعلومات الشخصية التي نجمعها:

• عندما تترك طلبًا على الموقع ، فقد نجمع معلومات مختلفة ، بما في ذلك اسمك ورقم هاتفك وعنوان بريدك الإلكتروني وما إلى ذلك.

كيف نستخدم المعلومات الشخصية الخاصة بك:

• تسمح لنا المعلومات الشخصية التي نجمعها بالاتصال بك والإبلاغ عن العروض الفريدة والعروض الترويجية والأحداث الأخرى والأحداث القادمة.
• من وقت لآخر ، قد نستخدم معلوماتك الشخصية لإرسال إشعارات ورسائل مهمة.
• يجوز لنا أيضًا استخدام المعلومات الشخصية للأغراض الداخلية ، مثل إجراء عمليات التدقيق وتحليل البيانات والأبحاث المختلفة من أجل تحسين الخدمات التي نقدمها وتزويدك بالتوصيات المتعلقة بخدماتنا.
• إذا شاركت في سحب على الجوائز أو مسابقة أو حدث ترويجي مشابه ، فقد نستخدم المعلومات التي تقدمها لإدارة مثل هذه البرامج.

إفشاء المعلومات لأطراف ثالثة

نحن لا نكشف عن المعلومات التي نتلقاها منك لأطراف ثالثة.

استثناءات:

• إذا كان من الضروري - وفقًا للقانون وأمر المحكمة و / أو إجراءات المحكمة و / أو بناءً على طلبات عامة أو طلبات من السلطات الحكومية في أراضي الاتحاد الروسي - الكشف عن معلوماتك الشخصية. قد نكشف أيضًا عن معلومات عنك إذا قررنا أن هذا الكشف ضروري أو مناسب للأمان أو لإنفاذ القانون أو لأسباب أخرى مهمة اجتماعيًا.
• في حالة إعادة التنظيم أو الدمج أو البيع ، يجوز لنا نقل المعلومات الشخصية التي نجمعها إلى جهة خارجية مناسبة - الخلف القانوني.

حماية المعلومات الشخصية

نحن نتخذ الاحتياطات - بما في ذلك الإدارية والفنية والمادية - لحماية معلوماتك الشخصية من الضياع والسرقة وسوء الاستخدام ، وكذلك من الوصول غير المصرح به والكشف والتعديل والتدمير.

احترام خصوصيتك على مستوى الشركة

من أجل التأكد من أن معلوماتك الشخصية آمنة ، فإننا نوفر قواعد السرية والأمان لموظفينا ، ونراقب بدقة تنفيذ تدابير السرية.

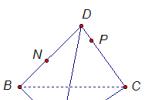
يرتبط اشتقاق مساحة n-gon المنتظم بنصف قطر الدائرة المدرجة في هذا n-gon ونصف قطر الدائرة المحصورة حولها. عند اشتقاق هذه الصيغة ، يتم استخدام تقسيم n-gon إلى n مثلثات. إذا كانت مساحة مضلع منتظم معين ، وجانبه ، هو المحيط ، وأنصاف أقطار الدوائر المنقوشة والمحددة ، على التوالي ، إذن. دعنا نثبت ذلك: من خلال ربط مركز مضلع معين برؤوسه ، كما هو موضح في الشكل 2.7.1 ، نقسمه إلى n مثلثات متساوية ، مساحة كل منها تساوي. بالتالي،. بالإضافة إلى ذلك،.

الشكل 2.7.1

الشكل 2.7.1

مثال 2.7.1.

يتم قطع هذا المربع الذي له جانب أ عند الزوايا بحيث يتشكل مثمن منتظم. حدد مساحة هذا الشكل الثماني.

القرار:

دع (الشكل 2.7.2). ثم من أين

الشكل 2.7.2

لذلك ، المنطقة المطلوبة

إجابة:

مثال 2.7.2.

ينقسم القوس الكامل لدائرة نصف قطرها R إلى أربعة أجزاء كبيرة وأربعة أجزاء صغيرة ، تتناوب الواحدة تلو الأخرى. معظمها ضعف حجمها الصغير. أوجد مساحة الشكل الثماني الذي تمثل رءوسه نقاط قسمة القوس الدائري.

القرار:

دع القوس الصغير يحتوي على درجات. ثم ، من حيث المعنى ، يحتوي الشكل الثماني على أربعة مثلثات بزاوية مركزية (مساحتها الإجمالية) وأربعة مثلثات بزاوية مركزية (مساحتها الإجمالية). المنطقة المطلوبة هي

إجابة:

مثال 2.7.3.

معطى مربع مع جانب. على كل جانب من جوانب المربع خارجه ، تم بناء شبه منحرف بحيث تشكل القواعد العلوية لهذه شبه المنحرف وجوانبها شكلًا منتظمًا. احسب مساحتها.

القرار:

المنطقة المراد البحث عنها ، وأين هي أنصاف أقطار دائرة محددة حول مربع وثنائي الأضلاع (الشكل 2.7.3). بما أن ضلع المربع متساوٍ إذن ... نملك أين⏊ لكن منذ ذلك الحين ... وهكذا ،

، بمعنى آخر

الشكل 2.7.3

إجابة:

3 مهام قياس التخطيط من الاختبار المركزي

الخيار 1

ال 8. في مثلث متساوي الساقين ، يتم رسم الخطوط المستقيمة و (D AB ؛ E AC) من خلال رؤوس القاعدة والنقطة (تقع على ارتفاع مرسوم على القاعدة ويقسمها فيما يتعلق بالعد من القاعدة). أوجد مساحة المثلث إذا كانت مساحة شبه المنحرف 64.

القرار:

دعنا نقدم الترميز:

يتبع من الشكل التالي

نصنع النظام:

الشكل 3.1

من النظام نحصل على:

لحل هذه المعادلة نجد:

بالتعويض في المعادلة الثانية للنظام ، نحصل على:

أوجد مساحة المثلث

إجابة:

الخيار 1

أ 8. في مثلث متساوي الساقين مع جوانب ، يتم رسم الارتفاع إلى الجانب. إذا كانت مراكز الدوائر مقيدة حول مثلثات ، فإن المسافة بين النقاط متساوية ...

القرار:

لا تذكر المشكلة بالتحديد ما هي الأطراف والقاعدة. إذا ، a ، فإن متباينة المثلث لن تصمد. وبالتالي و و. بعد ذلك ، عليك أن تتذكر حقيقة أن مركز الدائرة المحاطة بمثلث قائم الزاوية يقع في منتصف الوتر. لذلك ، فإن مراكز الدوائر محصورة حول المثلثات والنقاط ونقاط المنتصف على الجانبين وعلى التوالي.

الشكل 3.2

وهكذا ، هو الخط الأوسط للمثلث و

إجابة:

الخيار 1

ب4. الشكل الرباعي منقوش في دائرة. إذا كان ،، ثم قياس درجة الزاوية بين الخطوط المستقيمة يساوي ...

القرار:

منذ بشرط أن أعطينا ذلك ،، ثم نعلم أنه يمكن كتابة الشكل الرباعي في دائرة إذا وفقط إذا كانت مجموع زواياه المتقابلة متساوية.

الشكل 3.3

ويترتب على ذلك أنه من الممكن إيجاد الزاوية التي نحتاجها من المثلث. لذلك ، حصلنا على ذلك

إجابة:

الخيار 1

أ 12. القاعدة الأكبر لشبه المنحرف هي 114. أوجد القاعدة الأصغر لشبه المنحرف إذا كانت المسافة بين نقطتي منتصف قطريها هي 19.

القرار:

الشكل 3.4

دعونا نشير إلى القاعدة الأصغر من شبه المنحرف

مثلثات وما شابه. نحصل على النسبة:

من تشابه المثلثات نحصل على:

قسّم المعادلة الثانية على الأولى:

بالتالي:

نحصل على أن القاعدة الأصغر لشبه المنحرف هي

إجابة:

الخيار 1

أ 11. بالتوازي مع جانب المثلث ، يتم رسم خط مستقيم يتقاطع مع الضلع عند نقطة ما ... إذا كانت مساحة المثلث 50 ، فإن مساحة شبه المنحرف الناتجة هي ...

القرار:

الشكل 3.5

دعنا من هذا الشرط

ومن ثم ، إذن ، الآن نجد مساحة شبه المنحرف ، نحصل عليها

إجابة:

الخيار 1

أ 13. ارتفاع المثلث القائم الزاوية ، المرسوم على الوتر ، يقسمه إلى مقطع ، أطواله مرتبطة بـ 1: 4. إذا كان الارتفاع 8 ، فإن الوتر هو ...

القرار:

يمكن إيجاد طول ارتفاع المثلث القائم الزاوية المرسوم على الوتر بالصيغة:

صورة 3.6

حسب الشرط ، لقد أعطينا ذلك. بالتالي،

ومن ثم ، حصلنا على ذلك. ثم

إجابة:

الخيار 1

أ 12. تساوي قياسات زاويتين في المثلث و ، والارتفاع المرسوم من أعلى الزاوية الأكبر هو 9. أوجد الضلع الأصغر للمثلث.

القرار:

الشكل 3.7

اسمحوا ، يعني منذ-

ارتفاع المثلث. بما أن المثلث مستطيل ، فإن ضلع المثلث القائم الزاوية ، والذي يقع مقابل زاوية 30 ، يساوي نصف طول الوتر.

من العقار نحصل عليه:

إجابة:

الخيار 1

أ 16. يحتوي المعين المربع على دائرة مربعة. جانب المعين ...

القرار:

;

بما أن مساحة المعين تساوي الشرط ، إذن ثم،

من هذا حصلنا على ذلك

الشكل 3.8

إجابة:

الخيار 1

أ 11. رباعي ، فيه ، مرسوم في دائرة. أوجد درجة قياس الزاوية.

القرار:

يمكن كتابة الشكل الرباعي في دائرة إذا وفقط إذا كانت مجموع زواياه المتقابلة متساوية

الشكل 3.9

إجابة:

الخيار 1

على الساعة 3. قاعدة مثلث متساوي الساقين حاد الزاوية هي 10 وجيب الزاوية المقابلة هو. أوجد مساحة المثلث.

القرار:

الشكل 3.10

1. أوجد جيب تمام الزاوية بالصيغة

نظرًا لأن الزاوية حادة ، نختار العلامة "":

2. لإيجاد طول الضلع الجانبي (الشكل 3.10) ، طبق نظرية جيب التمام:

أو أور

3. أوجد مساحة المثلث بالصيغة:

;

إجابة: .

الخيار 1

المهمة B3. في دائرة نصف قطرها 6 ، يوجد مثلث منقوش ، أطوال ضلعيه 6 و 10. أوجد طول ارتفاع المثلث المرسوم إلى ضلعه الثالث.

القرار:

لننفذ رسمًا إضافيًا لحل المشكلة. اسمحوا ان يكون المثلث معطى.

لنرسم ارتفاع المثلث.

الشكل 3.11

في مثل هذه المهام ، فإن أصعب لحظة هي فهم كيفية ربط معلمات المثلث (الزوايا أو الجوانب) بمعلمات الدائرة. بعد كل شيء ، نحل مشكلة المثلث ، ولكن نظرًا لإعطاء نصف قطر الدائرة المقيدة ، يجب استخدامه بطريقة ما للحصول على المعلومات المفقودة حول المثلث نفسه.

تم إثبات إحدى أشهر الروابط بين المثلث والدائرة في نظرية الجيب. دعونا نكتب استنتاجات هذه النظرية للزاوية:

هذا هو نصف قطر الدائرة المحصورة حول المثلث. من هنا نحصل على:

أوجد الارتفاع من مثلث قائم الزاوية:

كرر المواد

مضلع منتظم يسمى مضلع محدب له جوانب متساوية وزوايا متساوية.

أ - جانب المثمن ،

R هو نصف قطر الدائرة المحددة ،

r هو نصف قطر الدائرة المنقوشة.

مجموع الزوايا الداخلية لـ n-gon منتظم

180 (ن -2).

قياس درجة الزاوية الداخلية لـ n-gon

180 (ن -2): ن.

جانب من n-ka الصحيح

نصف قطر دائرة منقوشة في مضلع منتظم

منطقة n-ka الصحيحة

تمارين

1-أ) مجموع الزوايا الداخلية للشكل السداسي هو:
1) 360 درجة ؛ 2) 180 درجة ؛ 3) 720 درجة ؛ 4) 540 درجة.
ب) مجموع الزوايا الداخلية للمثمن هو:
1) 360 درجة ؛ 2) 180 درجة ؛ 3) 720 درجة ؛ 4) 1080 درجة.
القرار:
أ) وفقًا للصيغة ، فإن مجموع زوايا الشكل السداسي هو: 180 (6-2) \u003d 180 * 4 \u003d 720 ° .
الجواب: 720 ° .


2. أ) طول ضلع المضلع العادي 5 سم ، والزاوية الداخلية 144°
أ) طول ضلع المضلع المنتظم 7 سم ، والزاوية الداخلية 150° ... أوجد محيط المضلع.
القرار:
أ) 1) أوجد عدد جوانب المضلع:
144 \u003d 180 (ن - 2): ن ؛
144 ن \u003d 180 ن -360 ؛
36 ن \u003d 360 ؛
ن \u003d 10.
2) أوجد محيط عشري الأضلاع: P \u003d 5 * 10 \u003d 50 cm.
الجواب: 50 سم.


3. أ) محيط الشكل الخماسي المنتظم يساوي 30 سم ، أوجد قطر الدائرة المحاطة بالخماسي.
ب) قطر الدائرة 10 سم ، أوجد محيط الخماسي المكتوب فيها.
القرار:
أ) 1) أوجد ضلع البنتاغون: 30: 5 \u003d 6 سم.
2) أوجد نصف قطر الدائرة المحددة:
أ \u003d 2R * الخطيئة (180 ° : ن)؛
6 \u003d 2R * الخطيئة (180 ° :5);
R \u003d 3: sin 36 ° \u003d 3: 0.588 \u003d 5.1 سم
الجواب: 5.1 سم.


4.أ) مجموع الزوايا الداخلية لمضلع منتظم هو 2520°
ب) مجموع الزوايا الداخلية لمضلع منتظم 1800° ... أوجد عدد أضلاع المضلع.
القرار:
أ) أوجد عدد جوانب المضلع:
2520 ° = 180 ° (ن -2) ؛
2520 ° +360 ° =180 ° ن؛
2880 ° =180 ° ن؛
ن \u003d 16.
الجواب: 16 جانب.


5. أ) نصف قطر دائرة محددة حول اثني عشر أضلاع منتظم هو 5 سم ، أوجد مساحة المضلع.
ب) نصف قطر دائرة حول مثمن منتظم يساوي 6 سم ، أوجد مساحة المضلع.
القرار:
أ) أوجد مساحة الدوديكون:
S \u003d 0.5 * R 2 * n * sin (360° : n) \u003d 0.5 * 25 * 12 * sin30° \u003d 75 سم 2 .
الجواب: 75 سم 2 .


6. أوجد مساحة الشكل السداسي إذا كنت تعرف مساحة الجزء المظلل:

القرار:
أ) 1) أوجد طول الضلع AB في الشكل السداسي. اعتبر المثلث ABC - متساوي الساقين (AB \u003d BC).
∠ABS \u003d 180 ° (6-2):6=120 ° .

مساحة المثلث ABC تساوي 0.5 * AB * BC * sin120° ويساوي 48 شرطًا.

2) في الشكل السداسي المنتظم ، يكون الضلع مساويًا لنصف قطر الدائرة المحصورة ، وبالتالي R \u003d AB.
3) أوجد مساحة الشكل السداسي:
الجواب: 288 سم 2 .

7.a) أوجد عدد أضلاع المضلع العادي إذا كان زاويته الخارجية عند القمة 18° .
ب) أوجد عدد أضلاع المضلع المنتظم إذا كان ركنه الخارجي عند القمة 45° .
القرار:
أ) مجموع الزوايا الخارجية لمضلع منتظم هو 360 ° .
أوجد عدد الأضلاع: 360 ° :18 ° =20.
الجواب: 20 جانب.


8. احسب مساحة الحلقة إذا كان الوتر AB يساوي:
أ) 8 سم ؛ ب) 10 سم.

القرار:
و)

1) ОВ - نصف قطر الدائرة الخارجية ، ОН - نصف قطر الدائرة الداخلية. يمكن إيجاد مساحة الحلقة بالصيغة: S ring \u003d S الخارجي دائرة - S دائرة داخلية.

S \u003d π * OB 2 - π * أوه 2 = π (OB 2 -يا 2 ).

2) النظر في المثلث ABO - متساوي الساقين ((А \u003d ОВ مثل نصف قطر). OH هو الارتفاع والوسيط في مثلث ABO ، لذلك ، AH \u003d HB \u003d 8: 2 \u003d 4 cm.

3) النظر في مثلث ONV - مستطيل: HB 2 \u003d OB 2 -HE 2 ، بالتالي

OV 2 -HE 2 =16.

4) ابحث عن منطقة الحلبة:

S \u003dπ (OB 2 -يا 2 )=16 π سم 2 .

إجابة:16 π سم 2 .

9.أ) أوجد محيط الشكل السداسي المنتظم إذا كان AC \u003d 9 سم.
ب) أوجد مساحة الشكل السداسي المنتظم إذا كانت FA \u003d 6 سم.

القرار:
أ) 1) أوجد الزاوية ABC: 180 ° (6-4):6=120 ° .
2) اعتبر المثلث ABC - متساوي الساقين (AB \u003d BC كأضلاع لشكل سداسي منتظم).
∠ أنت \u003d ∠ BCA \u003d (180° -120 ° ):2=30 ° .
حسب نظرية الجيب: AC: sin ∠ ABC \u003d AB: الخطيئة∠ BCA.
AB \u003d AC * sin30 ° : sin120؛

3) أوجد محيط الشكل السداسي المنتظم:

P \u003d 6 * AB ؛

10. إثبات أن مساحة الجزء المعبأ في الشكل المثمن العادي تساوي:
أ) ربع مساحة المثمن ؛ ب) نصف مساحة المثمن:

القرار:
و)

1) ارسم منصفات زوايا الشكل الثماني ، وسوف تتقاطع عند النقطة O. مساحة الشكل الثماني تساوي مجموع مساحات المثلثات الثمانية الناتجة المتساوية ، أي S (ABCDEFKM) \u003d 8 * S (OEF).

2) رباعي الزوايا ABEF - متوازي الأضلاع (AB // EF و AB \u003d EF). أقطار متوازي الأضلاع متساوية: AE \u003d BF (حيث أن أقطار الدائرة مقيدة حول مثمن) ، لذلك ABEF عبارة عن مستطيل. تقسم أقطار المستطيل إلى أربعة مثلثات متساوية.

3) أوجد مساحة رباعي الزوايا AFKM:

S (ABEF) \u003d 4 * S (OEF).

2 * S (AFKM) \u003d S (ABCDEFKM) - S (ABEF) \u003d 8 * S (OEF) -4 * S (OEF) \u003d 4 * S (OEF).

S (AFKM) \u003d 2 * S (OEF).

4) أوجد نسبة مساحة المثمن إلى مساحة الجزء المعبأ:

S (ABCDEFKM): S (AFKM) \u003d 8 * S (OEF): (2 * S (OEF)) \u003d 4.

Q.E.D.

11. أوجد نسبة مساحة قطاع BAC إلى مساحة الشكل المملوء إذا كانت BA \u003d AC ومساحة قطاع BAC تساوي ربع مساحة الدائرة:

القرار:
و)

1) AB \u003d AC \u003d 2R. زاوية أنت مستقيمة ، لأن مساحة قطاع BAC تساوي ربع مساحة الدائرة .

2) النظر في Quadrangle AO 2 MO 1 . إنه ألماس لأن كل الأضلاع تساوي نصف القطر ، ومنذ ذلك الحين إحدى زواياهما 90 درجة ، ثم AO 2 MO 1 - ميدان.

مثلث S \u003d 0.5 ص 2 سم 2 .
المقطع S \u003d (0.25 π - 0.5) R 2 سم 2.
الجزء المظلل S \u003d 2 * المقطع S \u003d 2 * (0.25 π - 0.5) ر 2 \u003d(0,5 π -1) ص 2 ثانيةم 2.
4) أوجد منطقة قطاع BAC:
سالقطاعات \u003dπ * (2R) 2 *90:360= π ر 2 من عندم 2.
5) أوجد نسبة مساحة قطاع BAC إلى مساحة الجزء المظلل:
π ر 2 :(0,5 π -1) ص 2= 2 π : (π-2).
إجابة: 2 π : (π-2).

مهام الحل المستقل

1. ما هو مجموع الزوايا الخارجية للبنتاغون؟

2. ما مساحة المثمن إذا كانت مساحة المساحة المعبأة 20.

3. محيط الشكل الرباعي العادي 20 سم ، أوجد طول الدائرة المنقوشة.

4. طول الضلع AB في المضلع العادي 8 سم. O هو مركز المضلع ، والزاوية AOB هي 36° ... أوجد محيط المضلع.

5. محيط الشكل الثماني المنتظم يساوي 80 cm ، أوجد قطره الأصغر.

6. دائرة منقوشة في مثلث عادي ودائرة موصوفة حولها. أوجد مساحة الحلقة المكونة من الدوائر إذا كان ضلع المثلث 8 سم.

7. أوجد الزاوية بين قطرين أصغر تمتد من رأس واحد من سباعي منتظم.

8. يوصف المثلث المنتظم بالقرب من الدائرة ويوجد فيه شكل سداسي منتظم. أوجد النسبة بين مساحة المثلث والسداسي.

9. المضلع المحدب له 48 جانبًا. أوجد عدد أقطارها.

10. ABCD عبارة عن مربع. يتم رسم دوائر نصف القطر AB من الرؤوس B و C. أوجد نسبة مساحة الشكل المملوء إلى مساحة المربع:

مثلث ، مربع ، مسدس - هذه الأشكال معروفة للجميع تقريبًا. لكن لا يعرف الجميع ما هو المضلع المنتظم. ولكن هذا هو نفس المضلع العادي يسمى المضلع الذي له زوايا وجوانب متساوية. هناك الكثير من هذه الأشكال ، لكن جميعها لها نفس الخصائص ، وتنطبق عليها نفس الصيغ.

خصائص المضلع المنتظم

يمكن كتابة أي مضلع منتظم ، سواء كان مربعًا أو مثمنًا ، في دائرة. غالبًا ما تُستخدم هذه الخاصية الأساسية عند إنشاء شكل. بالإضافة إلى ذلك ، يمكن كتابة دائرة في شكل مضلع. في هذه الحالة ، سيكون عدد نقاط الاتصال مساويًا لعدد جوانبها. من المهم أن يكون للدائرة المدرجة في مضلع منتظم مركز مشترك معها. هذه الأشكال الهندسية تخضع لنفس النظريات. يرتبط أي جانب من جوانب n-gon العادي بنصف قطر الدائرة المحصورة R. لذلك ، يمكن حسابه باستخدام الصيغة التالية: a \u003d 2R ∙ sin180 °. من خلال يمكنك العثور ليس فقط على الجوانب ، ولكن أيضًا على محيط المضلع.

كيفية إيجاد عدد أضلاع مضلع منتظم

يتكون أي واحد من عدد من الأجزاء المتساوية ، والتي ، عند الاتصال ، تشكل خطًا مغلقًا. في هذه الحالة ، كل زوايا الشكل المُشكَّل لها نفس القيمة. تنقسم المضلعات إلى بسيطة ومعقدة. تتضمن المجموعة الأولى مثلثًا ومربعًا. المضلعات المعقدة لها جوانب أكثر. وتشمل أيضا شخصيات على شكل نجمة. بالنسبة للمضلعات المنتظمة المعقدة ، يتم العثور على الجوانب من خلال كتابتها في دائرة. هنا دليل. ارسم مضلعًا منتظمًا بعدد عشوائي من الأضلاع n. ارسم دائرة حوله. اضبط نصف القطر R. الآن تخيل أنك حصلت على بعض n-gon. إذا كانت نقاط أركانها تقع على دائرة ومتساوية مع بعضها البعض ، فيمكن إيجاد الجانبين بالصيغة: a \u003d 2R ∙ sinα: 2.

إيجاد عدد أضلاع مثلث منتظم منقوش

المثلث متساوي الأضلاع هو مضلع منتظم. تنطبق الصيغ عليه كما هو الحال بالنسبة للمربع و n-gon. يعتبر المثلث صحيحًا إذا كان له نفس الطول. في هذه الحالة ، الزوايا تساوي 60. لنقم ببناء مثلث بطول ضلع معطى a. بمعرفة متوسطها وارتفاعها يمكنك معرفة معنى أضلاعها. للقيام بذلك ، سنستخدم طريقة إيجاد الصيغة a \u003d x: cosα ، حيث x هو الوسيط أو الارتفاع. بما أن كل جوانب المثلث متساوية ، نحصل على أ \u003d ب \u003d ج. عندئذٍ ستكون العبارة التالية صحيحة: a \u003d b \u003d c \u003d x: cosα. وبالمثل ، يمكنك إيجاد قيمة أضلاع مثلث متساوي الساقين ، لكن x سيكون الارتفاع المعطى. في هذه الحالة ، يجب أن يُسقط بدقة على قاعدة الشكل. إذن ، بمعرفة الارتفاع x ، نجد الضلع a في المثلث متساوي الساقين بالصيغة a \u003d b \u003d x: cosα. بعد إيجاد قيمة a ، يمكنك حساب طول القاعدة c. دعونا نطبق نظرية فيثاغورس. سنبحث عن قيمة نصف القاعدة c: 2 \u003d √ (x: cosα) ^ 2 - (x ^ 2) \u003d √x ^ 2 (1 - cos ^ 2α): cos ^ 2α \u003d x tgα. ثم ج \u003d 2xtgα. بهذه الطريقة البسيطة ، يمكنك إيجاد عدد أضلاع أي مضلع منقوش.

حساب جوانب مربع منقوش في دائرة

مثل أي مضلع منتظم منقوش آخر ، المربع له جوانب وزوايا متساوية. تنطبق نفس الصيغ عليه بالنسبة للمثلث. يمكنك حساب جوانب المربع باستخدام قيمة القطر. دعنا نفكر في هذه الطريقة بمزيد من التفصيل. من المعروف أن القطر يقسم الزاوية إلى النصف. في البداية ، كانت قيمتها 90 درجة. وهكذا ، بعد القسمة ، يتكون اثنان وتكون زاياهما عند القاعدة تساوي 45 درجة. وفقًا لذلك ، سيكون كل جانب من المربع متساويًا ، أي: a \u003d b \u003d c \u003d q \u003d e ∙ cosα \u003d e√2: 2 ، حيث e هو قطري المربع ، أو قاعدة المثلث القائم الزاوية المتكونة بعد القسمة. هذه ليست الطريقة الوحيدة لإيجاد جوانب المربع. دعونا نكتب هذا الشكل في دائرة. بمعرفة نصف قطر هذه الدائرة R ، نجد ضلع المربع. سنحسبها على النحو التالي a4 \u003d R√2. يتم حساب أنصاف أقطار المضلعات المنتظمة بالصيغة R \u003d a: 2tg (360 o: 2n) ، حيث a هو طول الضلع.

كيفية حساب محيط n-gon

محيط n-gon هو مجموع أضلاعه. ليس من الصعب حسابها. للقيام بذلك ، تحتاج إلى معرفة معاني جميع الأطراف. توجد صيغ خاصة لبعض أنواع المضلعات. إنها تسمح لك بإيجاد المحيط بشكل أسرع. من المعروف أن أي مضلع منتظم له أضلاع متساوية. لذلك ، لحساب محيطه ، يكفي معرفة واحد منهم على الأقل. تعتمد الصيغة على عدد جوانب الشكل. بشكل عام ، يبدو الأمر كما يلي: P \u003d an ، حيث a هي قيمة الضلع ، و n هي عدد الزوايا. على سبيل المثال ، لإيجاد محيط الشكل الثماني العادي مع ضلع يبلغ 3 سم ، عليك ضربه في 8 ، أي P \u003d 3 ∙ 8 \u003d 24 سم ، وبالنسبة إلى الشكل السداسي الذي يبلغ ضلعه 5 سم ، نحسب كالتالي: P \u003d 5 6 \u003d 30 سم. كل مضلع.

إيجاد محيط متوازي أضلاع ومربع ومعين

اعتمادًا على عدد أضلاع المضلع المنتظم ، يتم حساب محيطه. هذا يجعل المهمة أسهل بكثير. في الواقع ، على عكس الشخصيات الأخرى ، في هذه الحالة لا تحتاج إلى البحث عن جميع جوانبها ، يكفي واحد. وفقًا للمبدأ نفسه ، نجد محيط المربعات ، أي المربع والمعين. على الرغم من حقيقة أن هذه أرقام مختلفة ، فإن المعادلة بالنسبة لهم هي نفسها P \u003d 4a ، حيث a هو ضلع. دعنا نعطي مثالا. إذا كان طول ضلع معين أو مربع يساوي 6 سم ، فسنوجد المحيط كما يلي: P \u003d 4 ∙ 6 \u003d 24 سم ، الأضلاع المتقابلة فقط من متوازي أضلاع متساوية. لذلك ، تم إيجاد محيطه بطريقة مختلفة. إذن ، علينا معرفة الطول a والعرض في الشكل. ثم نطبق الصيغة P \u003d (a + b) ∙ 2. متوازي الأضلاع ، حيث جميع الأضلاع والزوايا بينها متساوية ، يسمى المعين.

إيجاد محيط مثلث متساوي الأضلاع وقائم الزاوية

يمكن إيجاد محيط المحيط الصحيح بالصيغة P \u003d 3a ، حيث a هو طول الضلع. إذا كان غير معروف ، فيمكن العثور عليه عبر الوسيط. في المثلث القائم الزاوية ، الضلعان فقط متساويان في الأهمية. يمكن إيجاد الأساس من خلال نظرية فيثاغورس. بعد أن أصبحت قيم الأضلاع الثلاثة معروفة ، نحسب المحيط. يمكن إيجاده من خلال تطبيق الصيغة P \u003d a + b + c ، حيث a و b متساويان ، و c هي القاعدة. تذكر أنه في المثلث المتساوي الساقين ، أ \u003d ب \u003d أ ، إذن أ + ب \u003d 2 أ ، ثم ف \u003d 2 أ + ج. على سبيل المثال ، إذا كان طول ضلع مثلث متساوي الساقين 4 سم ، فسنوجد قاعدته ومحيطه. نحسب قيمة الوتر وفقًا لنظرية فيثاغورس c \u003d √a 2 + في 2 \u003d 16 + 16 \u003d √32 \u003d 5.65 سم ، والآن نحسب المحيط P \u003d 2 ∙ 4 + 5.65 \u003d 13.65 سم.

كيف تجد زوايا المضلع المنتظم

يحدث مضلع منتظم في حياتنا كل يوم ، على سبيل المثال ، مربع عادي ، مثلث ، مثمن. يبدو أنه لا يوجد شيء أسهل من بناء هذا الرقم بنفسك. لكن هذا فقط للوهلة الأولى. من أجل بناء أي n-gon ، تحتاج إلى معرفة قيمة زواياه. لكن كيف تجدهم؟ حتى العلماء القدماء حاولوا بناء مضلعات منتظمة. لقد خمّنوا أن يكتبوها في دوائر. ثم قاموا بتمييز النقاط الضرورية عليها ، وربطوها بخطوط مستقيمة. بالنسبة للأشكال البسيطة ، تم حل مشكلة البناء. تم الحصول على الصيغ والنظريات. على سبيل المثال ، كان إقليدس في عمله الشهير "التأسيس" منخرطًا في حل المشكلات لـ 3 و 4 و 5 و 6 و 15 غون. وجد طرقًا لبناءها وإيجاد الزوايا. دعونا نرى كيف نفعل هذا لـ 15-gon. تحتاج أولاً إلى حساب مجموع زواياه الداخلية. يجب عليك استخدام الصيغة S \u003d 180⁰ (n-2). إذن ، لدينا 15-gon ، وبالتالي فإن العدد n هو 15. عوض بالبيانات التي نعرفها في الصيغة ونحصل على S \u003d 180⁰ (15-2) \u003d 180⁰ х 13 \u003d 2340⁰. لقد أوجدنا مجموع قياسات الزوايا الداخلية لـ 15-gon. أنت الآن بحاجة إلى الحصول على قيمة كل منها. مجموع الزوايا 15 ، نجري العملية الحسابية 2340⁰: 15 \u003d 156⁰. هذا يعني أن كل زاوية داخلية هي 156 درجة ، والآن بمساعدة مسطرة وبوصلة ، يمكنك بناء 15-gon منتظم. ولكن ماذا عن n-gons الأكثر تعقيدًا؟ لقرون عديدة ، كافح العلماء لحل هذه المشكلة. تم العثور عليها فقط في القرن الثامن عشر بواسطة كارل فريدريش جاوس. كان قادرًا على بناء 65537-gon. منذ ذلك الحين ، تم اعتبار المشكلة رسميًا تم حلها بالكامل.

حساب زوايا n-gons بالراديان

بالطبع ، هناك عدة طرق للعثور على زوايا المضلعات. غالبًا ما يتم حسابها بالدرجات. ولكن يمكنك أيضًا التعبير عنها بالراديان. كيف افعلها؟ تحتاج إلى المضي قدما على النحو التالي. أولاً ، نحدد عدد أضلاع المضلع المنتظم ، ثم نطرح 2. لذلك ، نحصل على القيمة: n - 2. اضرب الفرق الموجود في الرقم n ("pi" \u003d 3.14). كل ما تبقى الآن هو قسمة الناتج الناتج على عدد الزوايا في n-gon. ضع في اعتبارك هذه الحسابات باستخدام مثال نفس الشكل السداسي. إذن ، الرقم n هو 15. لنطبق الصيغة S \u003d n (n - 2): n \u003d 3.14 (15 - 2): 15 \u003d 3.14 ∙ 13: 15 \u003d 2.72. هذه بالطبع ليست الطريقة الوحيدة لحساب الزاوية بالراديان. يمكنك ببساطة قسمة الزاوية بالدرجات على 57.3. بعد كل شيء ، هذا العدد بالضبط من الدرجات يعادل راديان واحد.

حساب قيمة الزوايا بالدرجات

بالإضافة إلى الدرجات والراديان ، يمكنك محاولة إيجاد قيمة زوايا المضلع المنتظم بالدرجات. هذا يفعل كما يلي. اطرح 2 من العدد الإجمالي للزوايا ، واقسم الفرق الناتج على عدد أضلاع المضلع المنتظم. نضرب النتيجة التي تم العثور عليها في 200. بالمناسبة ، لا يتم استخدام وحدة قياس الزوايا مثل الدرجات عمليًا.

حساب الزوايا الخارجية لـ n-gons

بالنسبة لأي مضلع عادي ، يمكنك أيضًا حساب الزاوية الخارجية بالإضافة إلى المضلع الداخلي. تم العثور على معناه بنفس الطريقة كما هو الحال مع الشخصيات الأخرى. لذا ، للعثور على الزاوية الخارجية لمضلع منتظم ، عليك معرفة قيمة الضلع الداخلي. علاوة على ذلك ، نعلم أن مجموع هاتين الزاويتين يساوي دائمًا 180 درجة. لذلك ، نقوم بالحسابات على النحو التالي: 180 درجة ناقص قيمة الزاوية الداخلية. جد الفرق. ستكون مساوية لقيمة الزاوية المجاورة. على سبيل المثال ، الزاوية الداخلية للمربع 90 درجة ، إذن الخارج سيكون 180 درجة - 90 درجة \u003d 90 درجة. كما نرى ، ليس من الصعب العثور عليه. يمكن أن تأخذ الزاوية الخارجية قيمة من + 180 درجة إلى -180 درجة على التوالي.

نظرية 1. يمكن وصف دائرة حول أي مضلع منتظم.

لنفترض أن ABCDEF (شكل 419) هو شكل مضلع منتظم ؛ من الضروري إثبات أنه يمكن وصف دائرة حولها.

نعلم أنه يمكنك دائمًا رسم دائرة من خلال ثلاث نقاط لا تقع على خط مستقيم واحد ؛ ومن ثم ، يمكنك دائمًا رسم دائرة تمر عبر أي ثلاثة رؤوس لمضلع منتظم ، على سبيل المثال ، من خلال الرؤوس E و D و C. لتكن النقطة O مركز هذه الدائرة.

دعونا نثبت أن هذه الدائرة ستمر أيضًا من خلال الرأس الرابع للمضلع ، على سبيل المثال ، من خلال الرأس B.

المقاطع OE و OD و OS متساوية مع بعضها البعض ، وكل منها يساوي نصف قطر الدائرة. دعنا نرسم قطعة أخرى OB ؛ لا يمكن للمرء أن يقول على الفور عن هذا المقطع أنه يساوي أيضًا نصف قطر الدائرة ، يجب إثبات ذلك. ضع في اعتبارك المثلثات OED و ODC ، فهي متساوية الساقين ومتساوية ، لذلك ، ∠1 \u003d ∠2 \u003d ∠3 \u003d ∠4.

إذا كانت الزاوية الداخلية لهذا المضلع هي α ، فإن ∠1 \u003d ∠2 \u003d ∠3 \u003d ∠4 \u003d α / 2 ؛ ولكن إذا كانت ∠4 \u003d α / 2 ، فإن ∠5 \u003d α / 2 ، أي ∠4 \u003d ∠5.

ومن ثم ، فإننا نستنتج أن (دلتا) الوسواس القهري \u003d (دلتا) OCV ، وبالتالي ، ОВ \u003d ОВ ، أي أن الجزء يساوي نصف قطر الدائرة المرسومة. ويترتب على ذلك أن الدائرة ستمر أيضًا بالرأس B للمضلع المنتظم.

بالطريقة نفسها ، نثبت أن الدائرة المكونة سوف تمر عبر جميع الرؤوس الأخرى للمضلع. هذا يعني أن هذه الدائرة ستُحصر حول هذا المضلع المنتظم. تم إثبات النظرية.

نظرية 2. يمكن كتابة دائرة في أي مضلع منتظم.

لنفترض أن ABCDEF مضلع منتظم (الشكل 420) ، من الضروري إثبات إمكانية نقش دائرة فيه.

من المعروف من النظرية السابقة أنه يمكن وصف دائرة حول مضلع منتظم. لتكن النقطة O مركز هذه الدائرة.

قم بتوصيل النقطة O برؤوس المضلع. المثلثات الناتجة OED و ODC وما إلى ذلك متساوية مع بعضها البعض ، مما يعني أن ارتفاعاتها المرسومة من النقطة O متساوية أيضًا ، أي OK \u003d OL \u003d ОМ \u003d ON \u003d OP \u003d OQ.

لذلك ، فإن الدائرة الموصوفة من النقطة O على أنها من المركز بنصف قطر يساوي المقطع OK سوف تمر عبر النقاط K و L و M و N و P و Q ، وستكون ارتفاعات المثلثات هي نصف قطر الدائرة. أضلاع المضلع متعامدة مع نصف القطر عند هذه النقاط ، لذا فهي مماس لهذه الدائرة. وهذا يعني أن الدائرة المبنية منقوشة في هذا المضلع المنتظم.

يمكن إجراء نفس البناء لأي مضلع منتظم ، وبالتالي ، يمكن كتابة دائرة في أي مضلع منتظم.

نتيجة. الدوائر المحددة حول مضلع منتظم والمدرجة فيه لها مركز مشترك.

تعريفات.

1. مركز المضلع المنتظم هو المركز المشترك للدوائر المحيطة بهذا المضلع والمنقوشة فيه.

2. يُطلق على عمودي يتم إسقاطه من مركز مضلع منتظم إلى جانبه اسم مضلع منتظم.

التعبير عن أضلاع المضلعات المنتظمة بدلالة نصف قطر الدائرة المحددة

باستخدام الدوال المثلثية ، يمكنك التعبير عن جانب أي مضلع منتظم بدلالة نصف قطر الدائرة الموصوفة حوله.

دع AB يكون جانب الصحيح ن-درجت في دائرة نصف قطرها OA \u003d R (الشكل).

لنرسم حرف OD لمضلع منتظم ونفكر في مثلث قائم الزاوية AOD. في هذا المثلث

∠AOD \u003d 1/2 ∠AOB \u003d 1/2 360 درجة / ن \u003d 180 درجة / ن

AD \u003d AO sin ∠AOD \u003d R sin 180 ° / ن ;

لكن AB \u003d 2AD وبالتالي AB \u003d 2R sin 180 درجة / ن .

طول الجانب الأيمن ن-الرمز المدرج في دائرة عادة ما يشار إليه أ ن، لذلك يمكن كتابة الصيغة الناتجة على النحو التالي:

أ ن \u003d 2R sin 180 درجة / ن .

الآثار:

1. طول ضلع مسدس منتظم مرسوم في دائرة نصف قطرهار ، يتم التعبير عنها بالصيغة و 6 \u003d ص، مثل

و 6 \u003d 2R sin 180 ° / 6 \u003d 2R sin 30 ° \u003d 2R 1/2 \u003d R.

2. طول ضلع شكل رباعي منتظم (مربع) مرسوم في دائرة نصف قطرهار ، يتم التعبير عنها بالصيغة و 4 \u003d ص √2 ، مثل

و 4 \u003d 2R sin 180 ° / 4 \u003d 2R sin 45 ° \u003d 2R √ 2/2 \u003d R√2

3. طول ضلع مثلث منتظم مرسوم في دائرة نصف قطرهار ، يتم التعبير عنها بالصيغة و 3 \u003d ص √3 ، مثل.

و 3 \u003d 2R sin 180 ° / 3 \u003d 2R sin 60 ° \u003d 2R √ 3/2 \u003d R√3

منطقة المضلع المنتظم

دع الشخص الصحيح يعطى ن-غون (شكل). مطلوب لتحديد منطقته. دعونا نشير إلى جانب المضلع و والمركز من خلال O. نربطها بأجزاء المركز مع نهايات أي جانب من جوانب المضلع ، ونحصل على مثلث ، نرسم فيه مجموعة المضلع.

مساحة هذا المثلث هي آه / 2. لتحديد مساحة المضلع بالكامل ، تحتاج إلى ضرب مساحة مثلث واحد في عدد المثلثات ، أي في ن... نحصل على: S \u003d آه / 2 ن = اهن / 2 لكن ايساوي محيط المضلع. دعونا نشير إليه بقلم R.

أخيرًا نحصل على: S \u003d P ح / 2. حيث S هي مساحة المضلع المنتظم ، P هي محيطه ، ح - صيدلة.

مساحة المضلع المنتظم هي نصف حاصل ضرب محيطه وقطره.

مواد اخرى